数据结构 - 二叉树

之前的笔记搬运

二叉树

0x1 二叉树的类型

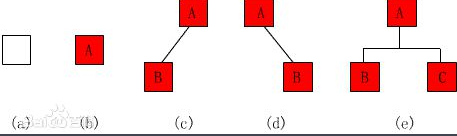
(1)空二叉树——如图(a)；

(2)只有一个根结点的二叉树——如图(b)；

(3)只有左子树——如图(c)；

(4)只有右子树——如图(d)；

(5)完整二叉树——如图(e)。

状态:

满二叉树:

除了叶节点,每个父亲节点都有两个子树的,满满的二叉树

完全二叉树:
所有节点集中在树左边的二叉树,就是说除了叶节点,每个节点都只有左节点或者有两个节点,而没有只有右节点情况

0x2相关术语

树的结点：
包含一个数据元素及若干指向子树的分支；

孩子结点：
结点的子树的根称为该结点的孩子；

双亲结点：
B 结点是A 结点的孩子，则A结点是B 结点的双亲；

兄弟结点：
同一双亲的孩子结点； 堂兄结点：同一层上结点；

祖先结点:
从根到该结点的所经分支上的所有结点子孙结点：以某结点为根的子树中任一结点都称为该结点的子孙

结点层：
根结点的层定义为1；根的孩子为第二层结点，依此类推；

树的深度：
树中最大的结点层

结点的度：
结点子树的个数

树的度：
树中最大的结点度。

叶子结点：
也叫终端结点，是度为 0 的结点；

分枝结点：
度不为0的结点；

有序树：
子树有序的树，如：家族树；

无序树：
不考虑子树的顺序；

0x3 二叉树性质

(1) 在非空二叉树中，第i层的结点总数不超过 , i>=1；

(2) 深度为h的二叉树最多有2\^h - 1 个结点，最少有h个结点；

(3) 具有n个结点的完全二叉树的深度为log(n+1)

0x4 二叉树的存储结构

• 数组 (只适合满二叉树, 不然浪费空间, 这里不谈)

• 链式存储, 一般会用一个结构体表示节点, 也称三叉链表

struct Tree

{
   Tree \* pParent; //父节点指针
   Tree \* pLeft; //左子树指针
   Tree \* pRight; //右子树指针
   TYPE Data; //数据
};

0x5 二叉树的遍历

遍历即将树的所有结点访问且仅访问一次。按照根节点位置的不同分为前序遍历，中序遍历，后序遍历。

前序遍历：根节点->左子树->右子树

中序遍历：左子树->根节点->右子树

后序遍历：左子树->右子树->根节点

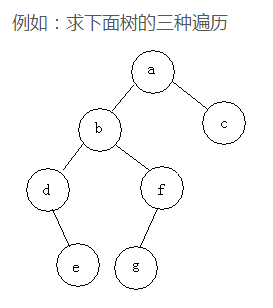
前: abdefgc

中: debgfac

后: edgfbca

赏

感谢大佬

微信